Demostrar que $\nabla r^n = n \cdot r^{n-2} \cdot \vec{r}$.
En primer lugar, definimos el gradiente de un vector como otro vector cuyas componentes son las derivadas parciales respecto de cada variable. Al tener solo una variable, $r$, la derivada parcial que tenemos es la siguiente:
\[\nabla r^n = n \cdot r^{n-1}\cdot \hat{r}\]Siendo $\hat{r}$ un vector unitario en la dirección y sentido de $\vec{r}$. Así pues, sabiendo que $\hat{r} = \frac{\vec{r}}{r}$, sustituimos y obtenemos lo siguiente:
\[\nabla r^n = n \cdot r^{n-1}\cdot \frac{\vec{r}}{r} = n \cdot r^{n-2} \cdot \vec{r}\]Como queríamos demostrar.
Hallar un vector unitario normal a la superficie $x^{2y} + 2xz = 2$.
Hemos de calcular el gradiente de $f(x,y,z) = x^{2y} + 2xz - 2$. El vector resultante es:
\[ \vec{\nabla} f = \left((2y - 1) \cdot x^{2y-1} + 2z, 2x^{2y} \cdot \ln{x}, 2x\right) \]Demostrar que $\nabla \cdot \left(\frac{\vec{r}}{r^3}\right) = 0$
Sabemos que si la divergencia de un campo es nula, el campo ha de ser gradiente de un campo $\phi$ escalar. En términos algebraicos:
\[ \frac{1}{r^2} \hat{r}= \left( \nabla \phi \right) \]Así,el campo escalar que buscamos es:
\[ \phi = \int \frac{1}{r^2} dr = -\frac{1}{r} + \mathcal{C} \]Por ende, hemos demostrado que el campo tiene divergencia nula.
Demostrar que $\nabla \cdot \left(f \vec{A}\right) = \left(\nabla f\right) \cdot \vec{A} + f \left(\nabla \vec{A}\right)$
En primer lugar, desarrollamos el paréntesis:
\[\nabla \cdot \left(f \vec{A}\right) = \nabla \cdot \left(f A_x + f A_y + f A_z\right)\]Aplicamos ahora el producto escalar:
\[\frac{\partial f}{\partial x} \cdot A_x + f \cdot \frac{\partial A_x}{\partial x} + \frac{\partial f}{\partial y} \cdot A_y + f \cdot \frac{\partial A_y}{\partial y} + \frac{\partial f}{\partial z} \cdot A_z + f \cdot \frac{\partial A_z}{\partial z}\]Reordenamos lo que tenemos y lo volvemos a poner como producto escalar:
\[(\nabla f) \cdot \vec{A} + f(\nabla \vec{A})\]Como queríamos demostrar.
Demostrar que $\nabla \times \left(f \vec{A}\right) = \left(\nabla f\right) \times \vec{A} + f \left(\nabla \times \vec{A}\right)$
En primer lugar, desarrollamos el paréntesis:
\[\nabla \times \left(f \vec{A}\right) = \nabla \times \left(f A_x + f A_y + f A_z\right)\]Aplicamos ahora el producto vectorial:
\[\begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ fA_x & fA_y & fA_z\\ \end{vmatrix} \]La primera componente del vector resultado es:
\[\frac{\partial}{\partial y} f(A_z) - \frac{\partial}{\partial z} f(A_y) = \left(\frac{\partial f}{\partial y} \cdot A_z - \frac{\partial f}{\partial z} \cdot A_y\right) + \left(\frac{\partial A_z}{\partial y} \cdot f - \frac{\partial A_y}{\partial z} \cdot f\right)\]En tal caso, el primer sumando de la derecha coincidiría con $(\nabla f) \times \vec{A}$ y el segundo con $f \left(\nabla \times \vec{A}\right)$, por lo que a sus primeras componentes respecta. Desarrollamos cada uno por separado y comprobamos si son iguales.
\[(\nabla f) \times \vec{A} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & \frac{\partial f}{\partial z}\\ A_x & A_y & A_z\\ \end{vmatrix} = \left(A_z \frac{\partial f}{\partial y} - A_y \frac{\partial f}{\partial z}\right) \hat{i} \quad ... \] \[f \left(\nabla \times \vec{A}\right) = f \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ A_x & A_y & A_z\\ \end{vmatrix} = \left(f \frac{\partial A_z}{\partial y} - f \frac{\partial A_y}{\partial z}\right) \hat{i} \quad ... \]Así pues, vemos que el desarrollo de la izquierda coincide, en su primera componente, con los desarrollos de la derecha. Esto es extrapolable a todas las componentes, demostrando la identidad.
Dado el campo vectorial $\vec{v} = \vec{\omega} \times \vec{r}$, siendo $\vec{\omega}$ constante, demostrar que $\vec{\omega} = \frac{1}{2} \nabla \times \vec{v}$.
Como $\vec{v} = \vec{\omega} \times \vec{r}$, sabemos que $\nabla \times \vec{v} = \nabla \times \left(\vec{\omega} \times \vec{r}\right)$. Calculamos el vector $\vec{\omega} \times \vec{r}$ y sacamos su rotacional. Obtenemos los resultados siguientes para el primer vector.
\[ \vec{\omega} \times \vec{r} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ \omega_x & \omega_y & \omega_j\\ x & y & z\\ \end{vmatrix} = \left(z\omega_y - y\omega_z;\ x\omega_z - z\omega_x;\ y\omega_x - x\omega_y\right) \]Sacamos el rotacional del vector resultado:
\[ \nabla \times \left(\vec{\omega} \times \vec{r}\right) = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ z\omega_y - y\omega_z & x\omega_z - z\omega_x & y\omega_x - x\omega_y\\ \end{vmatrix} = \] \[=\left(\frac{\partial}{\partial y}\left(y\omega_x - x\omega_y\right) - \frac{\partial}{\partial z}\left(x\omega_z - z\omega_x\right); \ \frac{\partial}{\partial z}\left(z\omega_y - y\omega_z\right) - \frac{\partial}{\partial x}\left(y\omega_x - x\omega_y\right);\ \frac{\partial}{\partial x}\left(x\omega_z - z\omega_x\right) - \frac{\partial}{\partial y} \left(z\omega_y - y\omega_z\right)\right) \]Algunas derivadas parciales se anulan y obtenemos el siguiente vector:
\[ \left(\omega_x + \omega_x; \ \omega_y + \omega_y; \ \omega_z + \omega_z\right) = \vec{\omega} + \vec{\omega} \]Como queríamos desmostrar.
Representar el vector $\vec{A} = z \hat{i} - x \hat{j} + y \hat{k}$ en coordenadas cilíndricas.
Sabemos, por definición, que:
\[x = \rho \cos \theta \qquad y = \rho \sin \theta \qquad z = z\]Así pues, sustituyendo, el vector $\vec{A}$ tendrá las siguientes componentes:
\[\vec{A} = z \hat{i} - \rho \cos \theta \hat{j} + \rho \sin \theta \hat{k} \tag{1} \label{eq:1}\]Ahora necesitamos cambiar los vectores unitarios. Sabemos que:
\[\hat{e_\rho} = \left(\cos \theta, \sin \theta, 0\right)\] \[\hat{e_\theta} = \left(-\sin \theta, \cos \theta, 0\right)\] \[e_z = \left(0, 0, 1\right)\]Haciendo las derivadas del vector $(x,y,z)$ con respecto a cada variable y dividiendo los resultados por su módulo.
De aquí, obtenemos las siguientes igualdades.
\[\hat{e_\rho} = \cos \theta \hat{i} + \sin \theta \hat{j} \label{eq:2} \tag{2}\] \[\hat{e_\theta} = -\sin \theta \hat{i} + \cos \theta \hat{j} \label{eq:3} \tag{3}\] \[e_z = \hat{k} \label{eq:4} \tag{4}\]Si multiplicamos $\eqref{eq:2}$ por $\cos{\theta}$ y $\eqref{eq:3}$ por $-\sin{\theta}$ para sumar las nuevas $\eqref{eq:2}$ y $\eqref{eq:3}$ obtenemos lo siguiente:
\[ \begin{cases} \cos \theta \cdot \hat{e_\rho} = \cos^2 \theta \hat{i} + \sin \theta \cdot \cos \theta \hat{j}\\ -\sin \theta \cdot \hat{e_\theta} = \sin^2 \theta \hat{i} - \sin \theta \cdot \cos \theta \hat{j} \end{cases} \]Sumando obtenemos que:
\[ \hat{i} = \cos{\theta} \cdot \hat{e_\rho} - \sin{\theta} \cdot \hat{e_\theta} \]Análogamente, multiplicamos a $\eqref{eq:3}$ por $\cos{\theta}$ y $\eqref{eq:2}$ por $\sin{\theta}$ para sumar las nuevas ecuaciones, obteniendo lo siguiente:
\[ \begin{cases} \sin \theta \cdot \hat{e_\rho} = \sin \theta \cdot \cos \theta \hat{i} + \sin^2 \theta \hat{j}\\ \cos \theta \cdot \hat{e_\theta} = -\sin \theta \cdot \cos \theta \hat{i} + \cos^2 \theta \hat{j} \end{cases} \]Sumando obtenemos que:
\[ \hat{j} = \sin{\theta} \cdot \hat{e_\rho} + \cos{\theta} \cdot \hat{e_\theta} \]Sustituyendo en $\eqref{eq:1}$ los últimos pasos:
\[\vec{A} = z \left(\cos{\theta} \cdot \hat{e_\rho} - \sin{\theta} \cdot \hat{e_\theta}\right) - \rho \cos \theta \left(\sin{\theta} \cdot \hat{e_\rho} + \cos{\theta} \cdot \hat{e_\theta}\right) + \rho \sin \theta \hat{e_z} \tag{1}\]Obtenemos que $\vec{A}$ es
\[ \vec{A} = \left(z \cos{\theta} - \rho \sin{\theta} \cos{\theta}, -z\sin{\theta} - \rho \cos^2{\theta}, \rho \sin{\theta}\right) \]Hallar el cuadrado del elemento de línea en coordenadas esféricas.
El elemento de línea en coordenadas esféricas tiene la forma siguiente:
\[ ds = h_r \: dr \:\hat{r} + h_\theta \: d\theta \:\hat{\theta} + h_\phi \: d\phi \:\hat{\phi} \]Donde $h_r = 1$, $h_\theta = r$ y $h_\phi = r\sin{\theta}$ son los factores de escala asociados a las coordenadas esféricas. Así pues,
\[ ds = 1 \: dr \:\hat{r} + r \: d\theta \:\hat{\theta} + r\sin{\theta} \: d\phi \:\hat{\phi} \]Elevando al cuadrado,
\[ (ds)^2 = 1 \: dr \:\hat{r} + r^2 \: d\theta \:\hat{\theta} + r^2\sin^2{\theta} \: d\phi \:\hat{\phi} \]Hallar las expresiones de los elementos de superficie en coordenadas curvilíneas ortogonales.
En un sistema de coordenadas curvilíneas tal que $x = x(u,v,w)$, $y = y(u,v,w)$ y $z = z(u,v,w)$ tenemos que los elementos de superficie respecto de cada variable son los factores de escala de las variables restantes por sus diferenciales. Así,
\[ dS_u = h_v \: h_w \: dv \: dw \qquad dS_v = h_u \: h_w \: du \: dw \qquad dS_w = h_v \: h_u \: dv \: du \]Por otra parte, conocemos que los factores de escala son:
\[ h_u = \left|\frac{\partial \vec{r}}{\partial u}\right| \qquad h_v = \left|\frac{\partial \vec{r}}{\partial v}\right| \qquad h_w = \left|\frac{\partial \vec{r}}{\partial w}\right| \]Siendo $\vec{r} = x \hat{i} + y\hat{j} + z \hat{k}$. Sustituyendo en los elementos:
\[ dS_u = \left|\frac{\partial \vec{r}}{\partial v}\right| \: \left|\frac{\partial \vec{r}}{\partial w}\right| \: dv \: dw \quad dS_v = \left|\frac{\partial \vec{r}}{\partial u}\right| \: \left|\frac{\partial \vec{r}}{\partial w}\right| \: du \: dw \quad dS_w = \left|\frac{\partial \vec{r}}{\partial v}\right| \: \left|\frac{\partial \vec{r}}{\partial u}\right| \: dv \: du \]Dado el vector $\vec{v} = (3,5)$, hallar las componentes bajo una rotación de $30º$ y comprobar que su módulo no varía.
Sabemos, por geometría, que, para cualquier ángulo de rotación las componentes nuevas $(x',y')$ serán:
\[ \begin{cases} x' = x \cos{\theta} + y \sin{\theta}\\ y' = y \cos{\theta} - x \sin{\theta} \end{cases} \]Podemos comprobar esto mediante la figura siguiente:
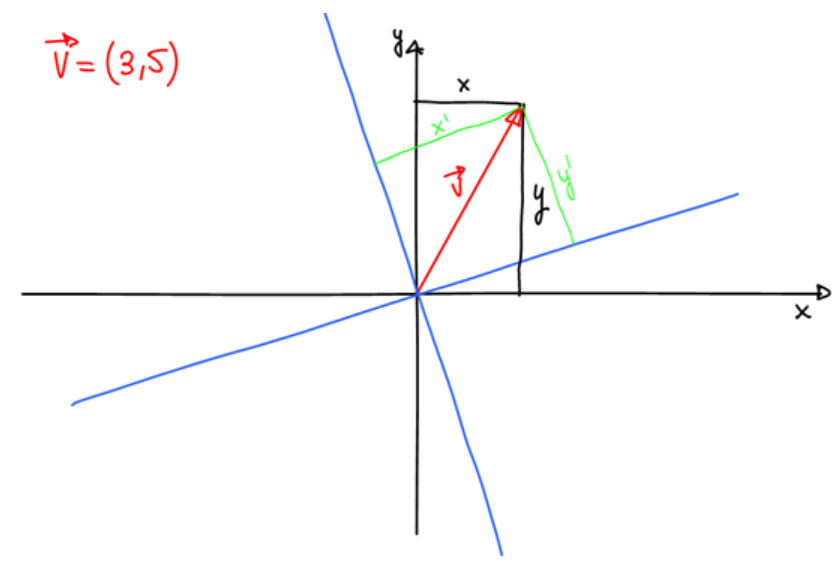
A la vista de lo especificado en el sistema de arriba, vemos que:
\[ \begin{cases} x' = \frac{\sqrt{3}}{2}x + \frac{1}{2}y\\ y' = \frac{\sqrt{3}}{2}y - \frac{1}{2}x \end{cases} \]Por lo que el vector tiene las siguientes componentes:
\[ \vec{v} = \left(\frac{5+3\sqrt{3}}{2}, \frac{5\sqrt{3}-3}{2}\right) \]Se puede comprobar que $v = \sqrt{34}$ en ambos casos.